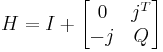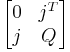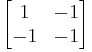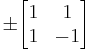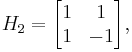Paley construction
In mathematics, the Paley construction is a method for constructing Hadamard matrices using finite fields. The construction was described in 1933 by the English mathematician Raymond Paley.
The Paley construction uses quadratic residues in a finite field GF(q) where q is a power of an odd prime number. There are two versions of the construction depending on whether q is congruent to 1 or 3 (mod 4).
Contents |
Quadratic character and Jacobsthal matrix
The quadratic character χ(a) indicates whether the given finite field element a is a perfect square. Specifically, χ(0) = 0, χ(a) = 1 if a = b2 for some non-zero finite field element b, and χ(a) = −1 if a is not the square of any finite field element. For example, in GF(7) the non-zero squares are 1 = 12 = 62, 4 = 22 = 52, and 2 = 32 = 42. Hence χ(0) = 0, χ(1) = χ(2) = χ(4) = 1, and χ(3) = χ(5) = χ(6) = −1.
The Jacobsthal matrix Q for GF(q) is the q×q matrix with rows and columns indexed by finite field elements such that the entry in row a and column b is χ(a − b). For example, in GF(7), if the rows and columns of the Jacobsthal matrix are indexed by the field elements 0, 1, 2, 3, 4, 5, 6, then
The Jacobsthal matrix has the properties QQT = qI − J and QJ = JQ = 0 where I is the q×q identity matrix and J is the q×q all-1 matrix. If q is congruent to 1 (mod 4) then −1 is a square in GF(q) which implies that Q is a symmetric matrix. If q is congruent to 3 (mod 4) then −1 is not a square, and Q is a skew-symmetric matrix. When q is a prime number, Q is a circulant matrix. That is, each row is obtained from the row above by cyclic permutation.
Paley construction I
If q is congruent to 3 (mod 4) then
is a Hadamard matrix of size q + 1. Here j is the all-1 column vector of length q and I is the (q+1)×(q+1) identity matrix. The matrix H is a skew Hadamard matrix, which means it satisfies H+HT = 2I.
Paley construction II
If q is congruent to 1 (mod 4) then the matrix obtained by replacing all 0 entries in
with the matrix
and all entries ±1 with the matrix
is a Hadamard matrix of size 2(q + 1). It is a symmetric Hadamard matrix.
Examples
Applying Paley Construction I to the Jacobsthal matrix for GF(7), one produces the 8×8 Hadamard matrix,
11111111 -1--1-11 -11--1-1 -111--1- --111--1 -1-111-- --1-111- ---1-111.
For an example of the Paley II construction when q is a prime power rather than a prime number, consider GF(9). This is an extension field of GF(3) obtained by adjoining a root of an irreducible quadratic. Different irreducible quadratics produce equivalent fields. Choosing x2+x−1 and letting a be a root of this polynomial, the nine elements of GF(9) may be written 0, 1, −1, a, a+1, a−1, −a, −a+1, −a−1. The non-zero squares are 1 = (±1)2, −a+1 = (±a)2, a−1 = (±(a+1))2, and −1 = (±(a−1))2. The Jacobsthal matrix is
It is a symmetric matrix consisting of nine 3×3 circulant blocks. Paley Construction II produces the symmetric 20×20 Hadamard matrix,
1- 111111 111111 111111 -- 1-1-1- 1-1-1- 1-1-1- 11 1-1111 ----11 --11-- 1- --1-1- -1-11- -11--1 11 111-11 11---- ----11 1- 1---1- 1--1-1 -1-11- 11 11111- --11-- 11---- 1- 1-1--- -11--1 1--1-1 11 --11-- 1-1111 ----11 1- -11--1 --1-1- -1-11- 11 ----11 111-11 11---- 1- -1-11- 1---1- 1--1-1 11 11---- 11111- --11-- 1- 1--1-1 1-1--- -11--1 11 ----11 --11-- 1-1111 1- -1-11- -11--1 --1-1- 11 11---- ----11 111-11 1- 1--1-1 -1-11- 1---1- 11 --11-- 11---- 11111- 1- -11--1 1--1-1 1-1---.
The Hadamard conjecture
The size of a Hadamard matrix must be 1, 2, or a multiple of 4. The Kronecker product of two Hadamard matrices of sizes m and n is an Hadamard matrix of size mn. By forming tensor products of matrices from the Paley construction and the 2×2 matrix,
Hadamard matrices of every allowed size up to 100 except for 92 are produced. In his 1933 paper, Paley says “It seems probable that, whenever m is divisible by 4, it is possible to construct an orthogonal matrix of order m composed of ±1, but the general theorem has every appearance of difficulty.” This appears to be the first published statement of the Hadamard conjecture. A matrix of size 92 was eventually constructed by Baumert, Golomb, and Hall, using a construction due to Williamson combined with a computer search. Currently, Hadamard matrices have been shown to exist for all 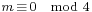 for m < 668.
for m < 668.
See also
References
- Paley, R.E.A.C. (1933). "On orthogonal matrices". Journal of Mathematics and Physics 12: 311–320.
- L. D. Baumert; S. W. Golomb, M. Hall Jr (1962). "Discovery of an Hadamard matrix of order 92". Bull. Amer. Math. Soc. 68 (3): 237–238. doi:10.1090/S0002-9904-1962-10761-7.
- F.J. MacWilliams; N.J.A. Sloane (1977). The Theory of Error-Correcting Codes. North-Holland. pp. 47,56. ISBN 0-444-85193-3.